


Next: Exercise 4.7: The solid
Up: Evaluation of observables
Previous: Exercise 4.5: Equation of
Although the use of periodic boundary conditions minimizes surface effects,
it is also important to choose the symmetry of the central ``unit cell'' to
be consistent with the symmetry of the solid phase of the system. This
choice of cell is essential if we wish to do simulations of the high
density, low-temperature behavior. We know that the equilibrium structure of
a crystalline solid at 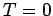 is the configuration of lowest energy.
is the configuration of lowest energy.
- Consider a triangular lattice of with
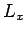 and height
and height
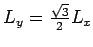 . Each column of the triangular lattice is separated by a distance
. Each column of the triangular lattice is separated by a distance 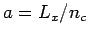 , where
, where 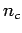 is the number of particles per row and
is the number of particles per row and 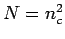 . For a square lattice to have the same density, we have to
choose the linear dimension to be
. For a square lattice to have the same density, we have to
choose the linear dimension to be
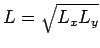 . Choose
. Choose 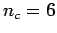 and
determine the energy for each lattice using the Lennard-Jones potential. Use
and
determine the energy for each lattice using the Lennard-Jones potential. Use
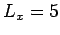 and
and 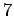 . What is the density of the system for each case? Are your
results for
. What is the density of the system for each case? Are your
results for 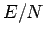 independent of the since of the lattice? Which lattice has
lower energy? Why?
independent of the since of the lattice? Which lattice has
lower energy? Why?
- Consider
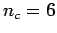 and
and 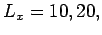 and
and 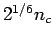 . Which lattice
structure has lowest energy in each case? In all these cases the net force
on a particle is zero. Why? The latter density correspond to the case where
the force between nearest neighbors is zero. Convince yourself that at this
density the lattice is unstable, since the force on any particle which
deviates from its equilibrium position in the lattice is negative.
Consequently, the system will collapse to a higher density, where the
triangular lattice is always favored.
. Which lattice
structure has lowest energy in each case? In all these cases the net force
on a particle is zero. Why? The latter density correspond to the case where
the force between nearest neighbors is zero. Convince yourself that at this
density the lattice is unstable, since the force on any particle which
deviates from its equilibrium position in the lattice is negative.
Consequently, the system will collapse to a higher density, where the
triangular lattice is always favored.
- Repeat the previous calculations for
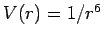 and
and 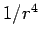 . Is
the triangular lattice still favored?
. Is
the triangular lattice still favored?



Next: Exercise 4.7: The solid
Up: Evaluation of observables
Previous: Exercise 4.5: Equation of
Adrian E. Feiguin
2004-06-01
![]() is the configuration of lowest energy.
is the configuration of lowest energy.