


Next: The continuum limit
Up: A one-dimensional random walk
Previous: Exercise 11.1: Random walks
- Consider a 1d random walk with jumps of all lengths allowed. The
probability that the length of a single step is
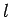 is denoted
is denoted 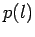 . If
the form of
. If
the form of 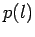 is given by
is given by 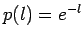 , what is the form of
, what is the form of
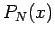 ? Suggestions: Use the inverse transform method explained in the
previous chapter to generate steps of length
? Suggestions: Use the inverse transform method explained in the
previous chapter to generate steps of length 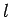 according to
according to 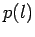 . Then
generate a walk of
. Then
generate a walk of 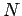 steps and determine the net displacement
steps and determine the net displacement 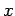 .
Generate many such walks and determine
.
Generate many such walks and determine 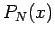 . Plot
. Plot 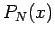 vs.
vs. 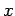 and
confirm that the form of
and
confirm that the form of 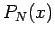 is consistent with a Gaussian
distribution.
is consistent with a Gaussian
distribution.
- Consider the step probability
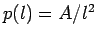 . Determine the
normalization constant
. Determine the
normalization constant 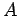 using:
using:
and the requirement that 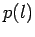 be normalized to unity. Perform a Monte
Carlo simulation as in part 1 and verify that the from of
be normalized to unity. Perform a Monte
Carlo simulation as in part 1 and verify that the from of 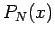 is
given by
is
given by
What is the magnitude of the constant 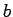 ? Does the variance of
? Does the variance of 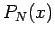 exist?
exist?
The ``central limit theorem'' states that the probability distribution of
a large number of measurements will be a Gaussian centered at the mean.
The only requirement is that the probability 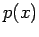 has finite first and
seconds moments, that the measurements are statistically independent, and
that
has finite first and
seconds moments, that the measurements are statistically independent, and
that 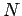 is large. In part 2 of the previous exercise, the probability
distribution has no second moment, and that explains the result.
is large. In part 2 of the previous exercise, the probability
distribution has no second moment, and that explains the result.



Next: The continuum limit
Up: A one-dimensional random walk
Previous: Exercise 11.1: Random walks
Adrian E. Feiguin
2004-06-01
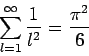
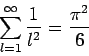
![]() has finite first and
seconds moments, that the measurements are statistically independent, and
that
has finite first and
seconds moments, that the measurements are statistically independent, and
that ![]() is large. In part 2 of the previous exercise, the probability
distribution has no second moment, and that explains the result.
is large. In part 2 of the previous exercise, the probability
distribution has no second moment, and that explains the result.