A one-dimensional random walk

Let us reformulate the previous problem in terms of diffusion of a molecule in a dilute gas. Suppose that the molecule travels a distance $l$ between collisions with other molecules. If we assume that the successive displacements of the molecule between collisions are statistically independent, then its motion is identical to the motion of the drunk. At each step he molecule has a probability $p$ to move to the right, and a probability $q=1-p$ to move to the left. If $n_{right}$ is the number of steps to the right, and $n_{left}$ the number of steps to the left, the total number of steps is going to be $N=n_{right}+n_{left}$, and the net displacement after $N$ steps will be $x=(n_{right}-n_{left})l$, with $-Nl \leq x \leq Nl$. The main quantity of interest will be the probability $P_N(x)$ for the molecule to be in position $x$ after $N$ steps. The mean net displacement $\langle x_N \rangle$ and the variance $\langle \Delta x_N^2 \rangle$ are going to be given by

$$\langle x_N \rangle = \sum_{x=-Nl}^{Nl}{xP_N(x)}$$

and

$$\langle \Delta x_N^2 \rangle = \langle x_N^2 \rangle - \langle x_N \rangle ^2$$

with

$$\langle x_N^2 \rangle = \sum_{x=-Nl}^{Nl}{x^2P_N(x)}.$$

all the averages are over all possible walks of $N$ steps. The analytical result can be obtained exactly for this case and the result is:

$$\langle x_N \rangle = (p-q)Nl$$

and

$$\langle \Delta x_N^2 \rangle = 4pqNl^2$$

Note that for the symmetrical case with $p=q=1/2$, the results is $\langle x_N \rangle = 0$. Now, let us identify these quantities for the case of the diffusion of the molecule. If $l$ is the mean free path, and $\tau$ the time between collisions, at a time $t$, the molecule would suffer $N=t/\tau$ collisions, obtaining

$$\langle \Delta x^2 \rangle = 4pql^2(t/\tau).$$

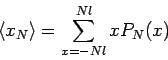
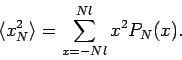
Since we know that the diffusion is characterize by the linear relation

$$\langle \Delta R(t)^2 \rangle = 2Dt,$$

where $D$ is the ``self-diffusion constant'', we obtain

$$D=2pql^2/\tau.$$

This is a very particular case that can be solved exactly. We need to develop a method to solve the general problem numerically. Two important approaches are exact enumeration and Monte Carlo methods.