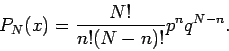in this approach, the number and probability of all walks for a given ![]() and
and ![]() are determined explicitly. Imagine that we represent by bits 0 and
1 as step to the right or left, respectively. The number of possible walks
with a given
are determined explicitly. Imagine that we represent by bits 0 and
1 as step to the right or left, respectively. The number of possible walks
with a given ![]() is going to be equivalent to the number of combinations
of
is going to be equivalent to the number of combinations
of ![]() bits, that is,
bits, that is, ![]() . The value of
. The value of ![]() for each
configuration of ones and zeroes is going to be given by the
difference between the number of ones and the number of zeroes. If
for each
configuration of ones and zeroes is going to be given by the
difference between the number of ones and the number of zeroes. If ![]() is
the number of ones, this is
is
the number of ones, this is
![]() . From here we obtain that
. From here we obtain that
![]() . The probability
. The probability ![]() for
each configuration will be given by
for
each configuration will be given by ![]() . Since the number of
configurations with a given
. Since the number of
configurations with a given ![]() or
or ![]() is
is
![]() , we obtain:
, we obtain: