


Next: Exercise 11.2: Random walk
Up: A one-dimensional random walk
Previous: Monte Carlo
- Implement a program to calculate the probabilities
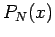 for a
given
for a
given 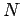 .
.
- Determine
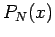 ,
,
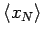 , and
, and
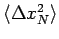 for
for 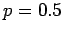 , and
, and 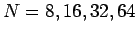 . Compare your results to the
exact answers.
. Compare your results to the
exact answers.
- Plot
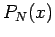 versus
versus 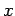 for the above values of
for the above values of 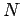 . Is
. Is 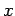 a
continuous function? What is the value of
a
continuous function? What is the value of 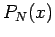 at its maximum for each
value of
at its maximum for each
value of 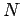 ? What is the approximate ``width'' of
? What is the approximate ``width'' of 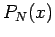 in each case?
in each case?
- Show from your previous plot that for sufficiently large
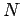 , the
computed distribution can be approximated by the Gaussian
, the
computed distribution can be approximated by the Gaussian
where
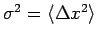 . Does the fit work equally
well for all
. Does the fit work equally
well for all 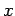 ?
?
- Suppose that
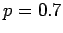 . Compute
. Compute
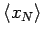 and
and
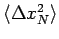 for the same values of
for the same values of 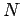 used in part 2. What is
the
interpretation of
used in part 2. What is
the
interpretation of
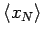 in this case?
in this case?
- Make a log-log plot of
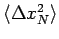 vs.
vs. 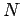 and
analyze the behavior for large.
and
analyze the behavior for large.
Many applications of random walk models make use of asymptotic behavior
for large 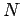 . For example in many random walk models,
. For example in many random walk models,
This is an example of a ``scaling law''. That is, if the number of steps
is doubled, the net mean square displacement increases by a factor
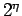 . For one-dimensional random walks we find from the exact
solution described above that
. For one-dimensional random walks we find from the exact
solution described above that 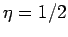 . If this kind of scaling law
exists, its exponent depends on the geometry of the lattice, as well as
the nature of the walk.
. If this kind of scaling law
exists, its exponent depends on the geometry of the lattice, as well as
the nature of the walk.



Next: Exercise 11.2: Random walk
Up: A one-dimensional random walk
Previous: Monte Carlo
Adrian E. Feiguin
2004-06-01
![\begin{displaymath}
P(x)=\sqrt{\frac{1}{2\pi \sigma^2}}\exp{[-(x-\langle x \rangle )^2/2
\sigma ^2]}
\end{displaymath}](img842.png)
![\begin{displaymath}
P(x)=\sqrt{\frac{1}{2\pi \sigma^2}}\exp{[-(x-\langle x \rangle )^2/2
\sigma ^2]}
\end{displaymath}](img842.png)
![]() . For example in many random walk models,
. For example in many random walk models,