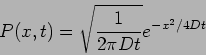Next: Two and three dimensional
Up: Random walks
Previous: Exercise 11.2: Random walk
Let us consider the continuum limit of the 1d random walk. If there is an
equal probability of taking a step to the right or left, the random walk
can be described by a simple ``master equation''
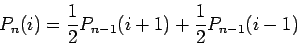 |
(105) |
where 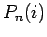 is the probability that the walker is at site
is the probability that the walker is at site 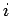 after
after 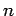 steps. In order to obtain a differential equation for the probability
density
steps. In order to obtain a differential equation for the probability
density 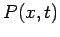 , we set
, we set 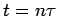 ,
, 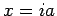 , and
, and
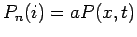 , where
, where
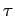 is the time between steps, and
is the time between steps, and 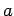 is the lattice spacing. Now we
can rewrite (106) as
is the lattice spacing. Now we
can rewrite (106) as
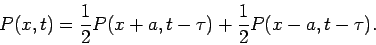 |
(106) |
We substract 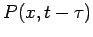 from both sides, we divide by
from both sides, we divide by 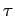 , and
rewrite (107) as:
, and
rewrite (107) as:
![\begin{displaymath}
\frac{P(x,t)-P(x,t-\tau)]}{\tau}=\frac{a^2}{2\tau}\frac{[P(x+a,t-\tau) %
- 2P(x,t-\tau)+P(x-a,t-\tau)]}{a^2}.
\end{displaymath}](img861.png) |
(107) |
Talking the limit
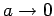 and
and
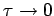 with the
ratio
with the
ratio 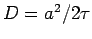 finite, we obtain the diffusion equation
finite, we obtain the diffusion equation
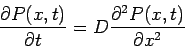 |
(108) |
The generalization to three dimensions is
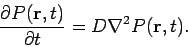 |
(109) |
This is the ``diffusion equation'' or ``Fokker-Planck equation'' and is
frequently used to describe the dynamics of fluid molecules.
The solution in free space can be shown to be a Gaussian
where 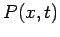 is the probability of finding a particle at position
is the probability of finding a particle at position 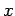 at
time
at
time 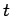 if is started from
if is started from 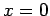 at
at 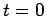 . From this equation we can
obtain:
. From this equation we can
obtain:
and
The generalization to 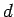 dimensions is
dimensions is
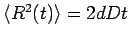 ,
where
,
where 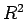 is the square of the displacement of the particle.
is the square of the displacement of the particle.



Next: Two and three dimensional
Up: Random walks
Previous: Exercise 11.2: Random walk
Adrian E. Feiguin
2004-06-01