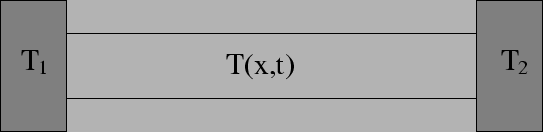Next: Finite differences solution
Up: P131-Computational Physics
Previous: Exercise 5.10: String with
The problems consiste in determining the temperature variation along
a bar of length  at any instant of time, given the initial gradient of
temperature.
at any instant of time, given the initial gradient of
temperature.
Figure 13:
A bar with the ends in contact with heat reservoirs.
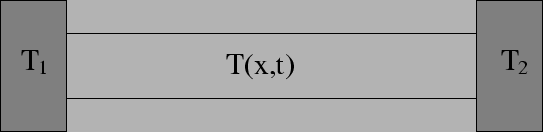 |
The problem is described by the ``Heat Equation'' that can be derived as follows:
At any instant of time, the heat flow through the bar equals the variatioon of energy inside the bar:
or
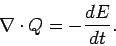 |
(60) |
The variation of the internal energy is given by the body's ability to store heat by raising its temperature:
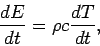 |
(61) |
where 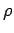 is the density, and
is the density, and 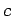 is the specific heat of the material.
Fourier's Law of heat conduction states that
is the specific heat of the material.
Fourier's Law of heat conduction states that
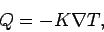 |
(62) |
where 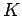 is the thermal conductivity.
Hence, we obtain
is the thermal conductivity.
Hence, we obtain
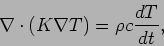 |
(63) |
or
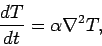 |
(64) |
with
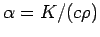 .
In 1d this equation is written
.
In 1d this equation is written
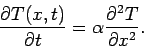 |
(65) |
We must solve this equation given the initial condition
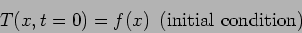 |
(66) |
and the boundary condition
Subsections



Next: Finite differences solution
Up: P131-Computational Physics
Previous: Exercise 5.10: String with
Adrian E. Feiguin
2004-06-01