


Next: Exercise 3.5: Resonance
Up: The harmonic oscillator
Previous: Exercise 3.3: Damped oscillations
How can we determine the period of a pendulum that is not already in
motion? The obvious way is to disturb the system, for instance, apply a
small displacement and observe the resulting motion. We will find that
the ``response'' of a system is actually an intrinsic property of the
system and can tell us about its nature in the absence of
perturbations.
Consider a damped linear oscillator with an external force 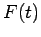
Is is customary to interpret the reponse of the system in terms of the
displacement 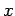 . The time dependence in
. The time dependence in 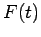 is arbitrary. A
particular case is when the force is harmonic:
is arbitrary. A
particular case is when the force is harmonic:
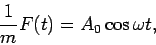 |
(42) |
where 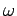 is the angular frequency of the driving force.
is the angular frequency of the driving force.
When a weak driving force has frequency 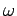 equal to the natural
frequency
equal to the natural
frequency 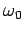 , it is possible to have a periodic steady motion
with frequency
, it is possible to have a periodic steady motion
with frequency 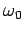 . In this case it is possible to pick the
magnitude of the external force such that after the initial transient
dies off, the average energy put into the system during one period
exactly balances the energy dissipated by friction. This leads to a
``limiting cycle'' in which the motion is stable even in the presence
of damping.
. In this case it is possible to pick the
magnitude of the external force such that after the initial transient
dies off, the average energy put into the system during one period
exactly balances the energy dissipated by friction. This leads to a
``limiting cycle'' in which the motion is stable even in the presence
of damping.
However, when the magnitude of the force 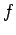 is large, the driving
overpowers the natural motion of the system and the steady state motion
is at the frequency of the driving force. This is a case of ``mode
locking''. The force can lock the system in an excited ``overtone'', a
vibrational mode with higher frequency. In this case the driving and
the natural frquencies are rationally related:
is large, the driving
overpowers the natural motion of the system and the steady state motion
is at the frequency of the driving force. This is a case of ``mode
locking''. The force can lock the system in an excited ``overtone'', a
vibrational mode with higher frequency. In this case the driving and
the natural frquencies are rationally related:
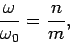
where 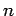 and
and 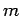 are integers.
are integers.
- Modify your program so that an external force of the form
(42) is included. Set
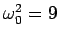 ,
, 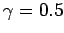 ,
,
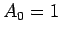 and
and 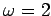 (we'll use these values fro the rest of the
exercise). These values correspond to a lightly damped oscillator. Plot
(we'll use these values fro the rest of the
exercise). These values correspond to a lightly damped oscillator. Plot
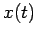 versus
versus 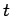 for the initial conditions
for the initial conditions 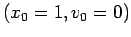 . How does
the qualitative behavior differ from the unperturbed case? What is the
period and angular frequency of
. How does
the qualitative behavior differ from the unperturbed case? What is the
period and angular frequency of 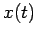 after several oscillations?
Obtain a similar plot with
after several oscillations?
Obtain a similar plot with 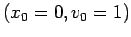 . What is the period and
angular frequancy after several oscillations? Does
. What is the period and
angular frequancy after several oscillations? Does
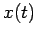 approach a limiting behavior that is independent of the initial
conditions? Identify a ``transient'' part of
approach a limiting behavior that is independent of the initial
conditions? Identify a ``transient'' part of 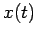 which depends on
the initial conditions and decays in time, and a ``steady state'' part
which dominates at longer times and which is independent of the initial
conditions.
which depends on
the initial conditions and decays in time, and a ``steady state'' part
which dominates at longer times and which is independent of the initial
conditions.
- Compute
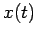 for
for 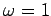 and
and 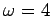 . What is the
period and angular frequancy of the steady state in each case?
. What is the
period and angular frequancy of the steady state in each case?
- Compute
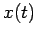 for
for 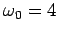 . What is the angular frequancy
of the steady state motion? Onthe basis of these results, explain which
parameters determine the frequency of the steady state behavior/
. What is the angular frequancy
of the steady state motion? Onthe basis of these results, explain which
parameters determine the frequency of the steady state behavior/
- Verify that the steady state behavior is given by
where 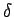 is the phase difference between the applied force and
the steady state motion. Compute
is the phase difference between the applied force and
the steady state motion. Compute 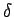 for
for
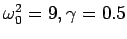 ,
,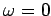 ,
,
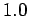 ,
, 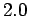 ,
, 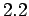 ,
, 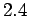 ,
, 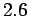 ,
, 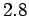 ,
, 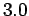 ,
, 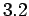 ,
, 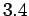 .
repeat the computation for
.
repeat the computation for 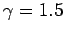 and plot
and plot 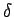 versus
versus
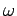 for the two values of
for the two values of 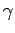 . Discuss the qualitative
dependence of
. Discuss the qualitative
dependence of
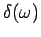 in the two cases.
in the two cases.



Next: Exercise 3.5: Resonance
Up: The harmonic oscillator
Previous: Exercise 3.3: Damped oscillations
Adrian E. Feiguin
2004-06-01
![]()
![]() equal to the natural
frequency
equal to the natural
frequency ![]() , it is possible to have a periodic steady motion
with frequency
, it is possible to have a periodic steady motion
with frequency ![]() . In this case it is possible to pick the
magnitude of the external force such that after the initial transient
dies off, the average energy put into the system during one period
exactly balances the energy dissipated by friction. This leads to a
``limiting cycle'' in which the motion is stable even in the presence
of damping.
. In this case it is possible to pick the
magnitude of the external force such that after the initial transient
dies off, the average energy put into the system during one period
exactly balances the energy dissipated by friction. This leads to a
``limiting cycle'' in which the motion is stable even in the presence
of damping.
![]() is large, the driving
overpowers the natural motion of the system and the steady state motion
is at the frequency of the driving force. This is a case of ``mode
locking''. The force can lock the system in an excited ``overtone'', a
vibrational mode with higher frequency. In this case the driving and
the natural frquencies are rationally related:
is large, the driving
overpowers the natural motion of the system and the steady state motion
is at the frequency of the driving force. This is a case of ``mode
locking''. The force can lock the system in an excited ``overtone'', a
vibrational mode with higher frequency. In this case the driving and
the natural frquencies are rationally related: