


Next: Exercise 3.4: Linear response
Up: The harmonic oscillator
Previous: Exercise 3.2: Large oscillations
If a drag force is included in the problem, the equation of motion
becomes:
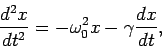
where the ``damping coefficient'' gamma is a measure of the friction.
Note that the drag force opposes the motion.
- Incorporate the effects of damping in yout program and plot the
time dependece of position and velocity. Make runs for
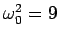 ,
,
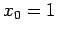 ,
, 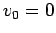 , and
, and 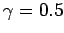 .
.
- Compare the period and angular frquency to the undamped case. is
the period longer or shorter? Make additional runs for
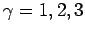 . Does the frequency increase or decrease with greater damping?
. Does the frequency increase or decrease with greater damping?
- Define the amplitude as the maximum value of
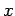 in one cycle.
Compute the ``relaxation time''
in one cycle.
Compute the ``relaxation time'' 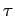 , the time it takes for the
amplitude to change from its maximum to
, the time it takes for the
amplitude to change from its maximum to
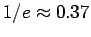 of its
maximum value. To do this, plot the maximum amplitud of each cycle, and
fit it with an exponential of the form
of its
maximum value. To do this, plot the maximum amplitud of each cycle, and
fit it with an exponential of the form
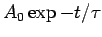 . Compute
. Compute
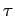 for each of the values of
for each of the values of 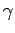 use in th previous item and
discuss the qualitative dependence of
use in th previous item and
discuss the qualitative dependence of 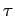 with
with 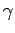 .
.
- Plot the total energy as a function of time for the
values of
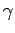 considered previously. If the decrease of the
energy is not monotonic, explainthe cause of the time-dependence.
considered previously. If the decrease of the
energy is not monotonic, explainthe cause of the time-dependence.
- Compute the average value of the kinetic energy, potential
energy, and total energy over a complete cycle. Plot these averages as
a function of the number of cycles. Due to the presence of damping,
these averages decrease with time. Is the decrease uniform?
- Compute the time-dependence of
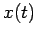 and
and 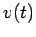 for
for
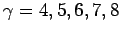 . Is the motion oscillatory for all
. Is the motion oscillatory for all 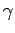 ?
Consider a condition for equilibrium
?
Consider a condition for equilibrium 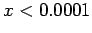 ; how quickly does
; how quickly does
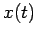 decay to equilibrium? For fixed
decay to equilibrium? For fixed 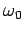 , the oscillator is
said to be ``critically damped'' at the smallest values of
, the oscillator is
said to be ``critically damped'' at the smallest values of 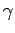 for
which the decay to equilibrium is monotonic. For what value of
for
which the decay to equilibrium is monotonic. For what value of 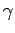 does critical damping occur for
does critical damping occur for 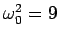 and
and 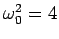 ? For
each value of
? For
each value of 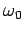 compute the value of
compute the value of 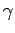 for which the
system approaches equilibrium more quickly.
for which the
system approaches equilibrium more quickly.
- Construct the phase space diagram for cases
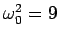 and
and
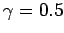 , 2, 4, 6, 8. Area the qualitative features of the paths
independent of
, 2, 4, 6, 8. Area the qualitative features of the paths
independent of 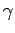 ? If not, discuss the qualitative differences.
? If not, discuss the qualitative differences.



Next: Exercise 3.4: Linear response
Up: The harmonic oscillator
Previous: Exercise 3.2: Large oscillations
Adrian E. Feiguin
2004-06-01