


Next: Exercise 3.3: Damped oscillations
Up: The harmonic oscillator
Previous: Exercise 3.1: Energy conservation
The pendulum responds to the equation of motion (40) only
in the limit of small angles. In the case of large oscillations, the
equation has to ve modified becoming
The enrgy of the pendulum is then given by
- Modify your program to simulate large amplitude
oscillations in a pendulum. Set
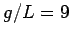 and choose
and choose 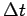 so that
the numerical solution is stable, i.e. it does no diverge with
time from the ``true'' solution. Check the stability by clculating the
total energy and ensuring thatt it does not drift from its initial
value.
so that
the numerical solution is stable, i.e. it does no diverge with
time from the ``true'' solution. Check the stability by clculating the
total energy and ensuring thatt it does not drift from its initial
value.
- Set
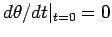 and make plots of
and make plots of 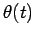 and
and
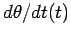 for the initial conditions
for the initial conditions
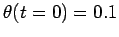 , 0.2, 0.4, 0.8, 1.0. Describle the qualitative
behavior
of
, 0.2, 0.4, 0.8, 1.0. Describle the qualitative
behavior
of 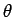 and
and 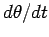 . What is the period
. What is the period 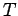 and the maximum
amplitude
and the maximum
amplitude 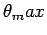 in each case? Plot
in each case? Plot 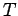 versus
versus 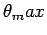 and
discuss the qualitative dependence of the period on the amplitude. How
do the results compare in the linear and non-linear cases, e.g.
which period is larger? Explain the relative values of
and
discuss the qualitative dependence of the period on the amplitude. How
do the results compare in the linear and non-linear cases, e.g.
which period is larger? Explain the relative values of 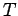 in physical
terms.
in physical
terms.



Next: Exercise 3.3: Damped oscillations
Up: The harmonic oscillator
Previous: Exercise 3.1: Energy conservation
Adrian E. Feiguin
2004-06-01