


Next: Chaotic structure in phase
Up: The harmonic oscillator
Previous: Exercise 3.4: Linear response
The long term behavior of the driven harmonic oscillator depends on the
frequency of the driving force. One measure of this behavior is the
maximum of the steady state displacement 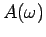 .
.
- Adopt the initial condition
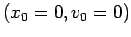 . Compute
. Compute 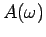 for
for 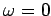 ,
, 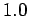 ,
, 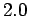 ,
,
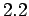 ,
, 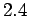 ,
, 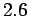 ,
, 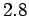 ,
, 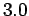 ,
, 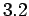 ,
, 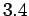 with
with 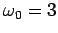 and
and 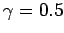 . Plot
. Plot 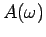 versus
versus 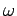 and describe its
qualitative behavior. If
and describe its
qualitative behavior. If 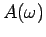 has a maximum, determine the
``resonance angular frequency''
has a maximum, determine the
``resonance angular frequency'' 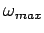 , which is the frequency
at the maximum of
, which is the frequency
at the maximum of 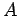 . Is the value of
. Is the value of 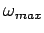 close to the
natural angular frequency
close to the
natural angular frequency 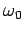 ?
?
- Compute
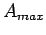 , the value of the amplitude at
, the value of the amplitude at 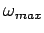 ,
and the ratio
,
and the ratio
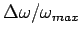 , where
, where 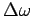 is
the ``width'' of the resonance. Define
is
the ``width'' of the resonance. Define 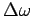 as the frequency
interval between points on the amplitude curve which are
as the frequency
interval between points on the amplitude curve which are
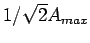 . Set
. Set 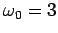 and consider
and consider
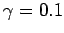 , 0.5, 1.0, 2.0. Describe the qualitative dependence of
, 0.5, 1.0, 2.0. Describe the qualitative dependence of
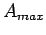 and
and
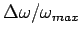 on
on 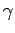 . The quantity
. The quantity
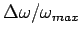 is proportional to
is proportional to 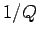 , where
, where 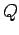 is
the ``quality factor'' of the oscillator.
is
the ``quality factor'' of the oscillator.
- Decribe the qualitative behavior of the steady state amplitude
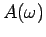 near
near 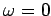 and
and
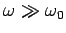 . Why is
. Why is
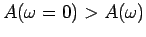 for small
for small 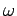 ? Why does
? Why does
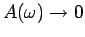 for
for
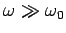 ?
?



Next: Chaotic structure in phase
Up: The harmonic oscillator
Previous: Exercise 3.4: Linear response
Adrian E. Feiguin
2004-06-01