4th order Runge-Kutta

Similar ideas can be used to derive a 3rd or 4th order Runge-Kutta method. It has been found by experience that the best balance between accuracy and computational effort is given by a fourth-order algorithm. Such a method would require evaluating $f$ four times at each step, with a local accuracy of $O(\Delta x^5)$. It can be written as follows:

$$k_1=\Delta x f(x_n,y_n),$$ (14)

$$k_2=\Delta x f(x_n+1/2\Delta x,y_n+1/2k_1),$$ (15)

$$k_3=\Delta x f(x_n+1/2\Delta x,y_n+1/2k_2),$$ (16)

$$k_4=\Delta x f(x_n+\Delta x,y_n+k_3),$$ (17)

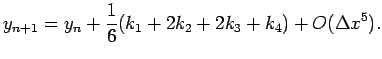$$y_{n+1}=y_n+\frac{1}{6}(k_1+2k_2+2k_3+k_4)+O(\Delta x^5).$$ (18)

Runge-Kutta method are self-staring, meaning that they can be used to obtain the first few iterations for a non self-starting algorithm.