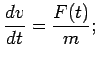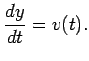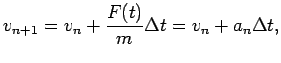Next: Exercise 1.2: One dimensional
Up: Ordinary differential equations: a
Previous: 4th order Runge-Kutta
We know that the motion of an object is determined by
Newton's equations. In the one-dimensional case, we can define the
instantaneous position 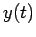 , velocity
, velocity 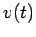 and acceleration
and acceleration 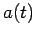 of an object using the language of differential calculus:
of an object using the language of differential calculus:
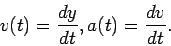 |
(19) |
The motion of the particle is defined by:
This is a second order differential equation that can written as
two first order differential equations:
| |
|
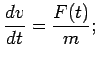 |
(20) |
| |
|
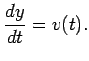 |
(21) |
To solve it we can apply any of the methods described in the previous
sections. If we pick Euler's, we obtain:
| |
|
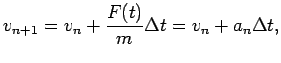 |
(22) |
| |
|
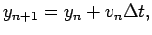 |
(23) |
where 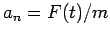 .
.
Subsections



Next: Exercise 1.2: One dimensional
Up: Ordinary differential equations: a
Previous: 4th order Runge-Kutta
Adrian E. Feiguin
2004-06-01