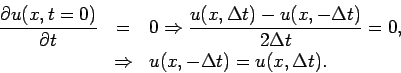To solve the equation (55) as a function of position and time we
need to discretize the ![]() space in a rectangular grid (see Fig 12). In the present case, the horizontal axis represents the position
space in a rectangular grid (see Fig 12). In the present case, the horizontal axis represents the position ![]() along the string, and the vertical axis represent time. We convert the
equation to a finite difference equation expressing the second derivatives
in terms of differences
along the string, and the vertical axis represent time. We convert the
equation to a finite difference equation expressing the second derivatives
in terms of differences
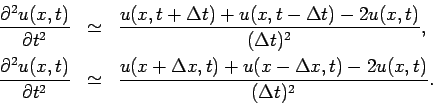
As shown in Fig. 12, this is a recurrence relation that propagates
the wave from the two earlier times ![]() and
and ![]() , and the three
nearby positions
, and the three
nearby positions ![]() ,
, ![]() , and
, and ![]() , to a later time
, to a later time ![]() , and a single position
, and a single position ![]() . We can see right a way that this is
not a self starting algorithm, in the sense that we need to know the
position fro two earlier times to start the iteration. However, we can use a
simple trick to overcome this difficulty. Rewriting the initial conditions (58) and (59) in the finite differences form, we
obtain:
. We can see right a way that this is
not a self starting algorithm, in the sense that we need to know the
position fro two earlier times to start the iteration. However, we can use a
simple trick to overcome this difficulty. Rewriting the initial conditions (58) and (59) in the finite differences form, we
obtain: