


Next: Numerical solution: finite differences
Up: Waves!
Previous: Exercise 5.8: Fourier analysis
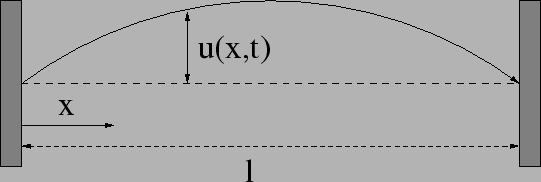
Figure 11:
A stretched string of length 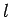 with the ends fixed.
with the ends fixed.
 |
The difference between waves and oscillatory motion is the scale. Waves are
the ``continuum'' limit of the problem, or in the jargon ``the long
wavelength'' limit. This is because in this limit, all the microscopic
details are ``washed out'' and only the long distance behavior survives. In
order to understand the transition between these two limits we have to
perform a change of scale. The discrete equations of motion, as shown
previously, can be written as:
We consider the limits
with the length of the chain kept constant. The main result is that in this
limit, the discrete equations of motion can me replaced by the continuous
wave equation:
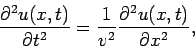 |
(54) |
where 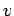 has the dimension of velocity and it is given by
has the dimension of velocity and it is given by
where 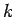 is the string tension and
is the string tension and 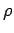 is the linear density. Observe
that the displacement
is the linear density. Observe
that the displacement 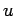 of the string is the dependent variable, and that
the position along the string
of the string is the dependent variable, and that
the position along the string 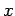 and the time
and the time 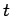 are the independent
variables. The existence of two independent variables makes this a Partial
Differential Equation (PDE).
are the independent
variables. The existence of two independent variables makes this a Partial
Differential Equation (PDE).
There are many solutions to this equation. Examples are:
In fact, it is easy to show that any function of the form 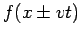 is a
solution. Since the differential equation is a linear equation and hence
satisfies the superposition principle, we can understand the behavior of a
wave of arbitrary shape using the Fourier's theorem to represent its shape
as a sum of sinusoidal waves.
is a
solution. Since the differential equation is a linear equation and hence
satisfies the superposition principle, we can understand the behavior of a
wave of arbitrary shape using the Fourier's theorem to represent its shape
as a sum of sinusoidal waves.
Because both ends of the string are tied down, the boundary conditions are:
Since this is a second order PDE, we still need to determine the initial
distortion 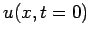 and velocity
and velocity
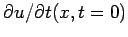 . If the
string is released from rest, this reduces to
. If the
string is released from rest, this reduces to
Subsections



Next: Numerical solution: finite differences
Up: Waves!
Previous: Exercise 5.8: Fourier analysis
Adrian E. Feiguin
2004-06-01

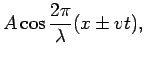
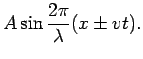
![]() and velocity
and velocity
![]() . If the
string is released from rest, this reduces to
. If the
string is released from rest, this reduces to