


Next: Runge-Kutta methods
Up: Ordinary differential equations: a
Previous: Higher order: Taylor's series
We can achieve higher accuracy by relating 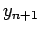 not only to
not only to 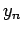 ,
but also to points further in the past
,
but also to points further in the past
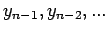 To derive
such formulas we can integrate exactly (1) to obtain:
To derive
such formulas we can integrate exactly (1) to obtain:
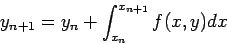 |
(9) |
The problem is that we don't know 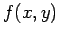 over the interval
over the interval
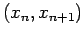 . However, we can use the values of
. However, we can use the values of 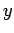 at
at 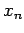 and
and
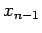 to provide a linear extrapolation:
to provide a linear extrapolation:
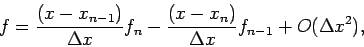 |
(10) |
with
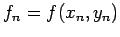 . Inserting into (9) we obtain
. Inserting into (9) we obtain
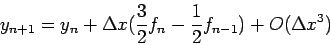 |
(11) |
Note that the value of 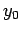 is not sufficient information to get this
algorithm started. The value of
is not sufficient information to get this
algorithm started. The value of 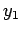 has to be obtained first by some
other procedure, like the ones described previously. This means that
the method is not ``self-starting''.
has to be obtained first by some
other procedure, like the ones described previously. This means that
the method is not ``self-starting''.
Adrian E. Feiguin
2004-06-01
![]() not only to
not only to ![]() ,
but also to points further in the past
,
but also to points further in the past
![]() To derive
such formulas we can integrate exactly (1) to obtain:
To derive
such formulas we can integrate exactly (1) to obtain:
![]() over the interval
over the interval
![]() . However, we can use the values of
. However, we can use the values of ![]() at
at ![]() and
and
![]() to provide a linear extrapolation:
to provide a linear extrapolation: