


Next: Multistep or Predictor-Corrector methods
Up: Ordinary differential equations: a
Previous: Exercise 1.1: Newton's law
We can go a step beyond Euler's method keeping up to second order
terms in the expansion around 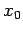 . Doing so we obtain
. Doing so we obtain
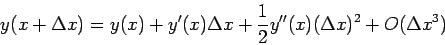 |
(5) |
from (1) we get
| |
|
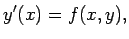 |
(6) |
| |
|
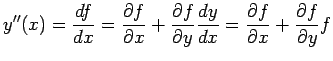 |
(7) |
Substituting in (5) we obtain
![\begin{displaymath}
y_{n+1}=y_n+f\Delta x+\frac{1}{2}(\Delta x)^2[\frac{\partial
f}{\partial x}+f\frac{\partial f}{\partial y}]+O(\Delta x^3),
\end{displaymath}](img41.png) |
(8) |
where all the functions and derivatives are evaluated in 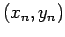 .
.
Adrian E. Feiguin
2004-06-01
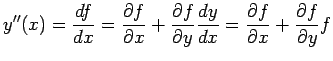
![\begin{displaymath}
y_{n+1}=y_n+f\Delta x+\frac{1}{2}(\Delta x)^2[\frac{\partial
f}{\partial x}+f\frac{\partial f}{\partial y}]+O(\Delta x^3),
\end{displaymath}](img41.png)