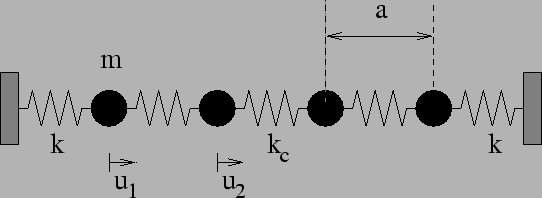
 |
Let us first consider a one-dimensional chain of ![]() particles of mass
particles of mass ![]() with equal equilibrium separation
with equal equilibrium separation ![]() . The particles are coupled to massless
springs with force constant
. The particles are coupled to massless
springs with force constant ![]() , except for the first and last springs
at the two ends of the chain which have spring constant
, except for the first and last springs
at the two ends of the chain which have spring constant ![]() . the individual
displacement of the particle
. the individual
displacement of the particle ![]() from its equilibrium position along the
from its equilibrium position along the ![]() axis is called
axis is called ![]() . The ends of the fist and last spring are assumed
fixed:
. The ends of the fist and last spring are assumed
fixed:
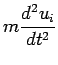 |
(46) | ||
| (47) |
The equations for particles ![]() and
and ![]() next to the walls are given by
next to the walls are given by
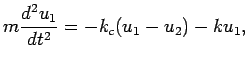 |
(48) | ||
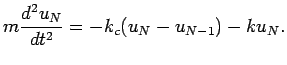 |
(49) |
Note that for ![]() all the equations will decouple and the motion of the
particles become independent of their neighbors. The above equations
describe longitudinal oscillations, i. e. motion along the
direction of the chain. The equations for transverse motion are equivalent.
all the equations will decouple and the motion of the
particles become independent of their neighbors. The above equations
describe longitudinal oscillations, i. e. motion along the
direction of the chain. The equations for transverse motion are equivalent.