MD simulation of Hard Spheres

To set the initial conditions let us consider the $N$ spheres to be distributed in a lattice, and with random initial velocities. An addtional requirement is that the total energy should be consistent with some desired temperature according to $E=3NkT/2$. Furthermore, is advantageous to make the total momentum (which will be conserved in the simulation) equal to zero.

Next, we compute for each pair of particles $(i,j)$ in the system the time $% t_{ij}$ that would take the pair to meet:

$$t_{ij}=\frac{-b-\sqrt{b^{2}-v^{2}(r^{2}-d^{2})}}{v^{2}}$$

where $d$ is the sphere diameter, $r$ is the distance between the centers of $i$ and $j$ , and

$$\begin{eqnarray*} b &=&(\mathbf{r}_{j}-\mathbf{r}_{i}).(\mathbf{v}_{j}-\mathbf{v... ...) \\ v &=&\left\vert (\mathbf{v}_{j}-\mathbf{v}_{i})\right\vert \end{eqnarray*}$$

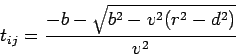
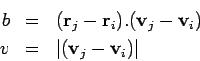
For each particle $i$ the smallest positive collision time $t(i)=\min (\{t_{ij}\})$ and the corresponding collision partner $j(i)$ are memorized. If the particle has no collision partner at positive times, we set $j(i)=-1$ and $t(i)=10^{16}$ or the largest representable number.

Evidently this calculation is quite costly, since there are $N(N-1)/2$ pairs to be scanned. However this double loop over all indices has to be performed only once, at the start of the simulation.

Next we identify the smallest among the $N$ ``next collision times'', calling it $t(i_{0}\dot{)}$ This will give us the time that will pass until the next collision occurring in the entire system. Let the partners in this collision be $i_{0}$ and $j_{0}$.

Now all the particle positions are incremented according to the free motion law

$$\mathbf{r}_{i}=\mathbf{r}_{i}+\mathbf{v}_{i}t(i_{0})$$

and all the $t(i)$ are decreased by $t(i_{0}).$

The elastic collision between the spheres $i=i_{0}$ and $j=j_{0}$ leads to new velocities of these two particles

$$\mathbf{v}_{i}^{\prime }=\mathbf{v}_{i}+\Delta \mathbf{v, v}% _{j}^{\prime }=\mathbf{v}_{j}-\Delta \mathbf{v}$$

where

$$\Delta \mathbf{v=}b\frac{\mathbf{r}_{ij}}{d^{2}}$$

All pairwise collision times $t_{ij}$ that involve either $i_{0}$ or $j_{0}$ must now be recalculated using the new velocities. For this purpose no more than $2N-3$ pairs have to be scanned.

The elementary step of a hard sphere MD calculations now completed. The next step is started by once more searching all the $t_{i}$ for the smallest element.