


Next: A mini solar system
Up: Kepler's problem
Previous: Astronomical units
- Write a program to simulate motion in a central force field.
Verify the case of circular orbit using (in astronomical units)
(
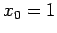 ,
, 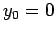 and
and 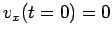 . Use the condition (32
to calculate
. Use the condition (32
to calculate 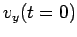 for a circular orbit. Choose a value of
for a circular orbit. Choose a value of 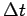 such that to a good approximation the total energy
such that to a good approximation the total energy 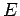 is
conserved. Is your value of
is
conserved. Is your value of 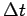 small enough to reproduce the
orbit over several periods?
small enough to reproduce the
orbit over several periods?
- Run the program for different sets of initial conditions
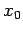 and
and 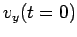 consistent with the condition for a circular orbit. Set
consistent with the condition for a circular orbit. Set 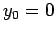 and
and
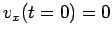 . For each orbit, measure the radius and the period to
verify Kepler's third law (
. For each orbit, measure the radius and the period to
verify Kepler's third law (
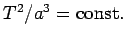 ). Think of a
simple condition which allows you to find the numerical value of the
period.
). Think of a
simple condition which allows you to find the numerical value of the
period.
- Show that Euler's method does not shield stable orbits for the
same choice of
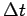 used in the previous items. Is it sufficient
to simply choose a smaller
used in the previous items. Is it sufficient
to simply choose a smaller 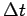 or Euler's method is no stable
for this dynamical system? Use the average velocity
or Euler's method is no stable
for this dynamical system? Use the average velocity
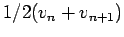 to obtain
to obtain 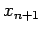 . Are the results any better?
. Are the results any better?
- Set
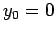 and
and 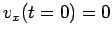 . By trial and error find several
choices of
. By trial and error find several
choices of 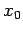 and
and 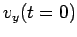 which yield coonvinient elliptical
orbits. Determine total energy, angular momentum, semi-major and
semi-nimor axes, eccentricity, and period for each orbit.
which yield coonvinient elliptical
orbits. Determine total energy, angular momentum, semi-major and
semi-nimor axes, eccentricity, and period for each orbit.
- You probably noticed that Euler's algorithm with a fixed
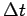 breaks down if you get to close to the sun. How are you able
to visually confirm this? What is the cause of the failure of the
method? Think of a simple modification of your program that can improve
your results.
breaks down if you get to close to the sun. How are you able
to visually confirm this? What is the cause of the failure of the
method? Think of a simple modification of your program that can improve
your results.



Next: A mini solar system
Up: Kepler's problem
Previous: Astronomical units
Adrian E. Feiguin
2004-06-01