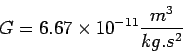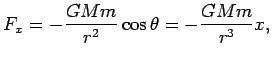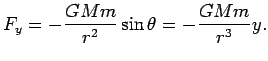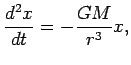Next: Circular motion
Up: Motion in a central
Previous: Motion in a central
The motion of the sun and the earth is an example of a ``two-body
problem''. This is a relatively simple problem that can be solved
analytically (it interesting to notice here, however, that adding a new
object to the problem, the moon for instance, make it completely
intractable. This is the famous ``three body problem'').
We can assume that,
to a good approximation, the sun is stationary and is a convenient
origin of our coordinate system. This is equivalent to changing to a
``center of mass'' coordinate system, where most of the mass is
concentrated in the sun. The problem can be reduced to an equivalent
one body problem involving an object of reduced mass 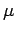 given by
given by
Since the mass of the earth is
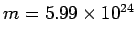 kg and the mass
of
the sun is
kg and the mass
of
the sun is
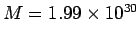 kg we find that for most practical
purposes, the reduced mass of the earth-sun system is
that of the earth. Hence, in the following we are going to consider the
problem of a single particle of mass
kg we find that for most practical
purposes, the reduced mass of the earth-sun system is
that of the earth. Hence, in the following we are going to consider the
problem of a single particle of mass 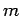 moving about a fixed center
of force, which we take as the origin of the coordinate system. The
gravitational force on the particle m is given by
moving about a fixed center
of force, which we take as the origin of the coordinate system. The
gravitational force on the particle m is given by
where the vector 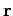 is directed from
is directed from 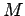 to
to 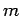 , and
, and 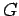 is
the gravitation constant
is
the gravitation constant
The negative sign implies that the gravitational force is attractive,
and decreases with the separation 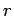 .
The gravitational force is a ``central force'': its magnitude depends on
the separation between the particles and its direction is along the
line that connects them. The assumption is that the motion is confined
to the
.
The gravitational force is a ``central force'': its magnitude depends on
the separation between the particles and its direction is along the
line that connects them. The assumption is that the motion is confined
to the 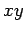 plane. The angular momentum
plane. The angular momentum 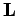 lies on the third
direction
lies on the third
direction 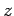 and is a constant of motion,
i.e. it is conserved:
and is a constant of motion,
i.e. it is conserved:
An additional constant of motion ins the total energy 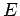 given by
given by
If we fix the coordinate system in the sun, the equation of motion is
For computational purposes it is convenient to write it down in
cartesian components:
| |
|
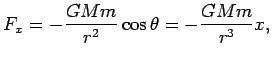 |
(28) |
| |
|
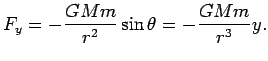 |
(29) |
Hence, the equations of motions in cartesian coordinates are:
| |
|
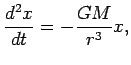 |
(30) |
| |
|
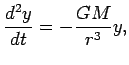 |
(31) |
where 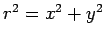 . These are coupled differential equations, since
each differential equation contains both
. These are coupled differential equations, since
each differential equation contains both 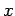 and
and 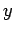 .
.
Subsections



Next: Circular motion
Up: Motion in a central
Previous: Motion in a central
Adrian E. Feiguin
2004-06-01