NORTHEASTERN UNIVERSITY
DEPARTMENT OF MATHEMATICS
Prof. Alex Suciu MTH 3481 - TOPOLOGY 3 Spring 1998
Take-Home Final Exam
Due Monday, June 15, at 9 AM
Instructions: Do 6 of the following 7 problems. Give complete proofs or justifications for each statement you make. Show all your work.
-
Let
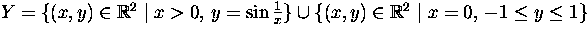 and
and 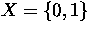 . Let
. Let 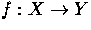 , given by f(0)=(0,0) and
, given by f(0)=(0,0) and 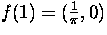 .
.
-
Show that
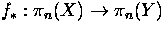 is an isomorphism, for all
is an isomorphism, for all 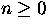 .
.
-
Show that f is not a homotopy-equivalence.
-
Does this contradict Whitehead's theorem? Why, or why not?
-
Let X be a connected, finite CW-complex, with
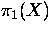 having a non-trivial element of finite order. Let
having a non-trivial element of finite order. Let 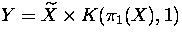 , where
, where 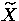 is the universal cover of X.
is the universal cover of X.
-
Show that
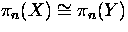 , for all n > 1.
, for all n > 1.
-
Show that X is not homotopy-equivalent to Y.
-
Does this contradict Whitehead's theorem? Why, or why not?
-
Let
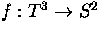 be the composite of the Hopf bundle map
be the composite of the Hopf bundle map 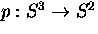 and the quotient map
and the quotient map 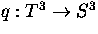 , which collapses the 2-skeleton of the 3-torus to a point.
, which collapses the 2-skeleton of the 3-torus to a point.
-
Show that
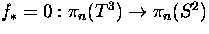 , for all
, for all 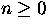 .
.
-
Show that
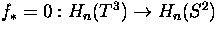 , for all
, for all 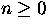 .
.
-
And yet f is not homotopic to a constant map.
-
Let X be a connected CW-complex, with
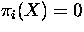 for 1 < i < n, for some n > 1. Let
for 1 < i < n, for some n > 1. Let 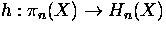 be the Hurewicz homomorphism. Show that
be the Hurewicz homomorphism. Show that 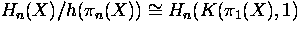 .
.
-
Let G be an abelian group.
-
Show that Hn+1(K(G,n))=0, for n > 1.
-
Show that there is a Moore space M(G,1) if and only if H2(K(G,1))=0.
-
For what values of n does there exist a Moore space of type
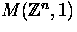 ?
?
-
Let
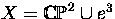 , with attaching map
, with attaching map 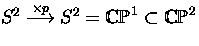 , and
, and 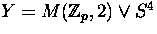 .
.
-
Show that
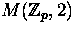 can be chosen so that X and Y have the same 3-skeleta.
can be chosen so that X and Y have the same 3-skeleta.
-
Show that
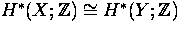 (as graded rings).
(as graded rings).
-
Show that
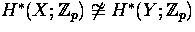 (as graded rings).
(as graded rings).
-
Let G be a group, and let
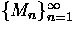 be a sequence of
be a sequence of 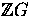 -modules.
-modules.
-
Construct a CW-complex X with
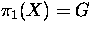 , and
, and 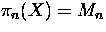 (as
(as 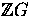 -modules).
-modules).
-
If
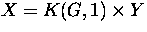 , where
, where 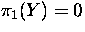 , show that
, show that 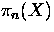 is trivial as a
is trivial as a 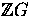 -module, for all n>1.
-module, for all n>1.
-
If
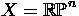 , show that
, show that 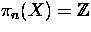 is trivial as a
is trivial as a 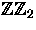 -module if and only if n is odd.
-module if and only if n is odd.
About this document ...
Back to MTH 3481, or back to my Home page.
Created by Alexandru I. Suciu, Wed Jun 10, 1998
 alexsuciu@neu.edu
alexsuciu@neu.edu
http://www.math.neu.edu/~suciu/mth3107/top3final/index.html
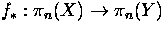 is an isomorphism, for all
is an isomorphism, for all 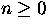 .
.
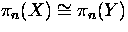 , for all n > 1.
, for all n > 1.
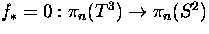 , for all
, for all 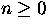 .
.
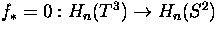 , for all
, for all 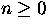 .
.
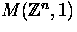 ?
?
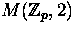 can be chosen so that X and Y have the same 3-skeleta.
can be chosen so that X and Y have the same 3-skeleta.
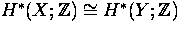 (as graded rings).
(as graded rings).
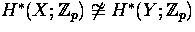 (as graded rings).
(as graded rings).
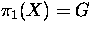 , and
, and 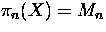 (as
(as 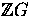 -modules).
-modules).
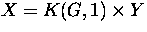 , where
, where 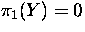 , show that
, show that 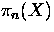 is trivial as a
is trivial as a 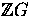 -module, for all n>1.
-module, for all n>1.
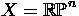 , show that
, show that 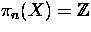 is trivial as a
is trivial as a 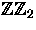 -module if and only if n is odd.
-module if and only if n is odd.
 alexsuciu@neu.edu
alexsuciu@neu.edu