- Show that each component of X is an open subset of X.
- Show that, if X is connected, then X is path-connected.
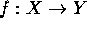 is bijective and continuous, show that f is a homeomorphism.
is bijective and continuous, show that f is a homeomorphism.
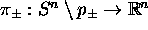 be the stereographic projections. Write down explicit
formulas for these maps, and prove that they are homeomorphisms.
be the stereographic projections. Write down explicit
formulas for these maps, and prove that they are homeomorphisms.
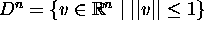 be the unit n-disk,
with boundary
be the unit n-disk,
with boundary 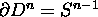 . Prove that
. Prove that
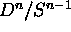 is homeomorphic to
is homeomorphic to 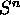 .
.
 on
on
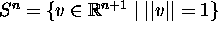 by writing
by writing
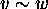 if and only if
if and only if
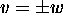 . The quotient space
. The quotient space
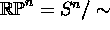 is called the (real) projective n-space.
Let
is called the (real) projective n-space.
Let 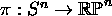 ,
,
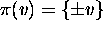 be the canonical
projection. For each i,
be the canonical
projection. For each i, 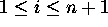 ,
define a subset
,
define a subset 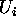 of
of
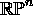 by
by
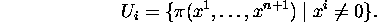
Prove the following facts, which together show that
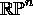 is an n-manifold.
is an n-manifold.
-
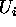 is open in
is open in
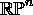 .
.
-
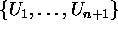 covers
covers 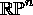 .
.
- There is a homeomorphism
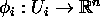 .
.
-
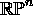 is compact, connected, and Hausdorff.
is compact, connected, and Hausdorff.
-
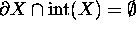 .
.
-
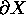 is an
is an
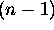 -manifold.
-manifold.
-
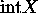 is an n-manifold.
is an n-manifold.
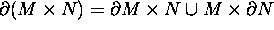 .
.
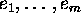 for V and
for V and
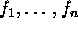 for W defines an isomorphism
of
for W defines an isomorphism
of 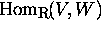 with the real vector space of
with the real vector space of
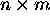 matrices with real coefficients,
matrices with real coefficients, 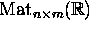 .
Shows that this isomorphism transforms composition
.
Shows that this isomorphism transforms composition
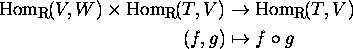
into matrix multiplication
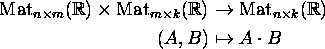
 alexsuciu@neu.edu
alexsuciu@neu.edu