NORTHEASTERN UNIVERSITY
DEPARTMENT OF MATHEMATICS
Prof. Alex Suciu
MTH 3107 - TOPOLOGY II Winter 1998
Take-Home Final Exam
Due Tuesday, March 17
Instructions:
Do at least 6 of the following 10 problems. Give complete proofs or
justifications for each statement you make. Show all your work.
- Let X=[0,1] and
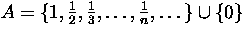 .
Is H1(X,A) isomorphic to
.
Is H1(X,A) isomorphic to
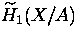 ? Explain why, or why not.
? Explain why, or why not.
-
- Let X and Y be two finite CW complexes. Show that
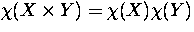 .
. - Let A and B
be two subcomplexes of X such that
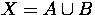 .
Show that
.
Show that 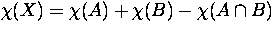 .
.
- Let
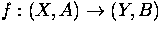 be a continuous map. Assume that
be a continuous map. Assume that
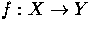 and
and 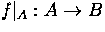 are homotopy equivalences.
are homotopy equivalences.
- Show that
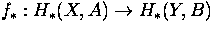 is an isomorphism.
is an isomorphism.
- Give an example where
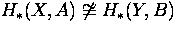 , although X is homotopy
equivalent to Y, and A is homotopy equivalent to B.
, although X is homotopy
equivalent to Y, and A is homotopy equivalent to B.
- Let
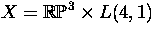 be the product of the projective
space
be the product of the projective
space 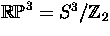 with the lens space
with the lens space
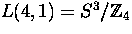 .
.
- Find a CW-decomposition of X.
- Determine the chain complex
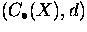 associated to
that cell decomposition.
associated to
that cell decomposition.
- Compute the homology groups H*(X).
- Let
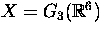 be the Grassmanian of 3-planes in
be the Grassmanian of 3-planes in
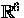 .
.
- Find a CW-decomposition of X.
- Determine the chain complex
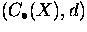 associated to
that cell decomposition.
associated to
that cell decomposition.
- Compute the homology groups H*(X).
- Let Tg be the orientable surface of genus g.
- Describe a 2-fold cover
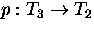 .
. - Compute
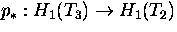 .
. - Compute
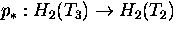 .
.
- Let
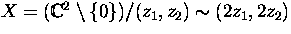 .
Compute H*(X).
.
Compute H*(X).
- Show that
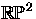 is not a retract of
is not a retract of
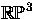 .
.
- Problem 1, in Bredon's book, p. 259.
- Problem 5, in Bredon's book, p. 259.
About this document ...
Back to
MTH 3107, or back to my
Home page.
Created by Alexandru I. Suciu, Sat Mar 21, 1998
 alexsuciu@neu.edu
alexsuciu@neu.edu
http://www.math.neu.edu/~suciu/mth3107/top2final/index.html
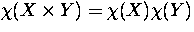 .
.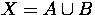 .
Show that
.
Show that 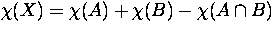 .
. 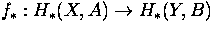 is an isomorphism.
is an isomorphism.
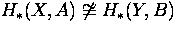 , although X is homotopy
equivalent to Y, and A is homotopy equivalent to B.
, although X is homotopy
equivalent to Y, and A is homotopy equivalent to B.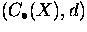 associated to
that cell decomposition.
associated to
that cell decomposition.
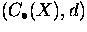 associated to
that cell decomposition.
associated to
that cell decomposition.
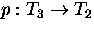 .
.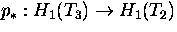 .
.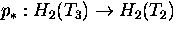 .
. alexsuciu@neu.edu
alexsuciu@neu.edu