


Next: Boundary conditions
Up: Monte Carlo Simulation
Previous: Exercise 13.1: Classical gas
Consider a lattice with 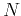 sites, where each site
sites, where each site 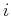 can assume two
possible states
can assume two
possible states 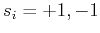 , or spin ``up'' and spin ``down''. A
particular configuration or microstate of the lattice is specified by the
set of variables
, or spin ``up'' and spin ``down''. A
particular configuration or microstate of the lattice is specified by the
set of variables
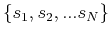 for all lattice sites.
for all lattice sites.
Now we need to know the dependence of the energy 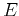 of a given microstate,
according to the configuration of spins. The total energy in the presence
of a uniform magnetic field is given by the ``Ising model'':
of a given microstate,
according to the configuration of spins. The total energy in the presence
of a uniform magnetic field is given by the ``Ising model'':
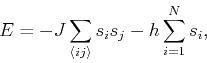 |
(276) |
where the first summation is over all nearest neighbor pairs and the
second summation is over all the spins of the lattice. The ``exchange
constant'' 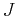 is a measure of the strength of the interaction between
nearest neighbor spins. If
is a measure of the strength of the interaction between
nearest neighbor spins. If 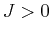 , the states with the spins
aligned
, the states with the spins
aligned
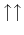 and
and
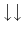 are energetically favored, while for
are energetically favored, while for 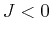 the
configurations with the spins antiparallel
the
configurations with the spins antiparallel
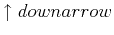 and
and
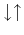 are the ones that are preferred. In the first case,
we expect that the state with lower energy is ``ferromagnetic'', while in
the second case, we expect it to be ``antiferromagnetic''. If we subject
the system to a uniform magnetic field
are the ones that are preferred. In the first case,
we expect that the state with lower energy is ``ferromagnetic'', while in
the second case, we expect it to be ``antiferromagnetic''. If we subject
the system to a uniform magnetic field 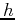 directed upward, the spins
directed upward, the spins
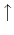 and
and 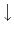 possess and additional energy
possess and additional energy 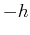 and
and 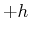 respectively. Note that we chose the units of
respectively. Note that we chose the units of 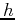 such that the magnetic
moment per spin is unity.
such that the magnetic
moment per spin is unity.
Instead of obeying Newton's laws, the dynamics of the Ising model
corresponds to ``spin flip'' processes: a spin is chosen randomly, and the
trial change corresponds to a flip of the spin
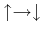 or
or
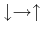 .
.
Subsections



Next: Boundary conditions
Up: Monte Carlo Simulation
Previous: Exercise 13.1: Classical gas
Adrian E. Feiguin
2009-11-04
![]() sites, where each site
sites, where each site ![]() can assume two
possible states
can assume two
possible states ![]() , or spin ``up'' and spin ``down''. A
particular configuration or microstate of the lattice is specified by the
set of variables
, or spin ``up'' and spin ``down''. A
particular configuration or microstate of the lattice is specified by the
set of variables
![]() for all lattice sites.
for all lattice sites.
![]() of a given microstate,
according to the configuration of spins. The total energy in the presence
of a uniform magnetic field is given by the ``Ising model'':
of a given microstate,
according to the configuration of spins. The total energy in the presence
of a uniform magnetic field is given by the ``Ising model'':
![]() or
or
![]() .
.