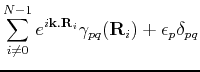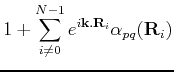Next: Example 5.1: Single s
Up: Methods for band-structure calculations
Previous: The tight-binding approximation
Let us consider a more general case, independently of the form of the Hamiltonian and the crystal structure. We are assuming for simplicity that we have one atom per unit cell (we shall see the generalization later), and the electron-electron interarctions are ignored.
We shall write the wave function for a single site, as a linear combinatioj of atomic orbitals
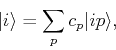 |
(186) |
wheer the coefficient 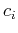 are unknown. We are also assuming that the different orbitals form a locally orthogonal basis:
are unknown. We are also assuming that the different orbitals form a locally orthogonal basis:
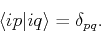 |
(187) |
This does not mean that the orbitals on different sites will not have a finite overlap.
Let us write a 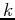 -state as:
-state as:
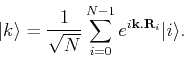 |
(188) |
We want to explicitly obtain a form for the eigenvalue equation
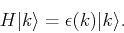 |
(189) |
Applying the Hamiltonian on the state 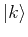 yields:
yields:
We now multiply from the left by 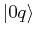 , to obtain
, to obtain
This leads to a generalized eigenvalue equation of the form
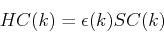 |
(193) |
in order to calculate the matrix elements explicitly, let us break 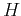 into a pice containing the atomic potential on site
into a pice containing the atomic potential on site 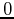 ,
, 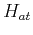 , and the remaning part in a term that we call
, and the remaning part in a term that we call 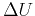 . Therefore, we obtain:
. Therefore, we obtain:
this yields
Subsections



Next: Example 5.1: Single s
Up: Methods for band-structure calculations
Previous: The tight-binding approximation
Adrian E. Feiguin
2009-11-04
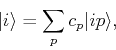
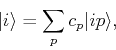
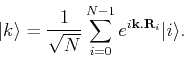
![]() yields:
yields:
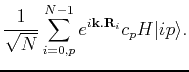
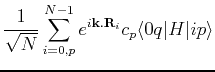
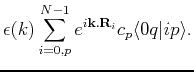
![]() into a pice containing the atomic potential on site
into a pice containing the atomic potential on site ![]() ,
, ![]() , and the remaning part in a term that we call
, and the remaning part in a term that we call ![]() . Therefore, we obtain:
. Therefore, we obtain: