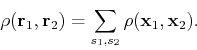Next: Hartree-Fock theory
Up: Many electron systems and
Previous: Two-particle case
When considering a many-electron system, we must remember that the electrons are identical particles. This is seen in the Hamiltonian, exchanging indices 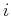 and
and 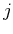 does not change the Hamiltonian. We say that the Hamiltonian commutes with the particle exchange operator
does not change the Hamiltonian. We say that the Hamiltonian commutes with the particle exchange operator 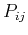 . This operator has the effect of exchanging the coordinates of particles
. This operator has the effect of exchanging the coordinates of particles 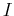 and
and 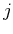 :
:
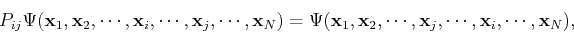 |
(90) |
where the coordinates 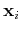 contain the orbital and spin part.
contain the orbital and spin part.
Since the Hamiltonian commutes with the operator 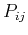 , its eigenvectors should simultaneously be eigenvectors of
, its eigenvectors should simultaneously be eigenvectors of 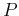 . Since
. Since 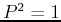 , its eigenvalues are either
, its eigenvalues are either 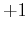 or
or 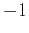 . In the first case, we say that the particles are bosons, while in the second case, we call them fermions. Since electrons are fermions, we find that their many-body wave-function whould be antisymmetric under exchanges.
. In the first case, we say that the particles are bosons, while in the second case, we call them fermions. Since electrons are fermions, we find that their many-body wave-function whould be antisymmetric under exchanges.
Let us forget about antisymmetry for a moment. For the case of an independent particle Hamiltonian, which is the sum of one-electron Hamiltonians, we can write the solution to the Schrödinger equation as a product of one-particle wave-functions:
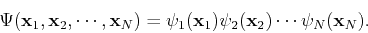 |
(91) |
the one-particle states are eigenstates of the one-particle Hamiltonians. The probability density id then given by
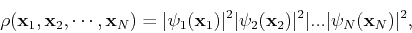 |
(92) |
which is just the product of one-particle densities. Such a probability density is called uncorrelated.
Of course, a state with the coordinates permuted is also a solution, as are linear combinations of such states. But the requirement of antisymmetry implies that the wave function should have the form:
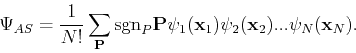 |
(93) |
P is a permutation operator that permutes the coordinates, and not the wave-functions. The sign in the sum can be 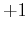 or
or 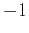 according to wether the permutation can be written as a product of even or odd pair interchanges, respectively.
according to wether the permutation can be written as a product of even or odd pair interchanges, respectively.
We can write this wave-function as a Slater determinant:
Its is important to note that after the antisymmetrization procedure the electrons are correlated. To see this we write the prbability density of finding two electrons with coordinates 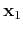 and
and 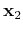 :
:
To find the probability of having two electrons at positions 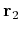 and
and 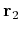 we have to sum over the spin variables:
we have to sum over the spin variables:
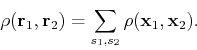 |
(96) |
We can see that for 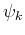 and
and 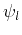 having opposite spin, the second term in (96) vanishes and therefore opposite spin oribitals are uncorrelated, but for equal spins, the two terms cancel when
having opposite spin, the second term in (96) vanishes and therefore opposite spin oribitals are uncorrelated, but for equal spins, the two terms cancel when
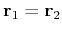 , so electrons with equal spins cannot sit on the same point in space and are kept apart. Every electron is found surrounded by an exchange hole in which other electrons having similar spin are hardly found. This is nothing else but a manifestation of Pauli's exclussion principle.
, so electrons with equal spins cannot sit on the same point in space and are kept apart. Every electron is found surrounded by an exchange hole in which other electrons having similar spin are hardly found. This is nothing else but a manifestation of Pauli's exclussion principle.



Next: Hartree-Fock theory
Up: Many electron systems and
Previous: Two-particle case
Adrian E. Feiguin
2009-11-04
![]() , its eigenvectors should simultaneously be eigenvectors of
, its eigenvectors should simultaneously be eigenvectors of ![]() . Since
. Since ![]() , its eigenvalues are either
, its eigenvalues are either ![]() or
or ![]() . In the first case, we say that the particles are bosons, while in the second case, we call them fermions. Since electrons are fermions, we find that their many-body wave-function whould be antisymmetric under exchanges.
. In the first case, we say that the particles are bosons, while in the second case, we call them fermions. Since electrons are fermions, we find that their many-body wave-function whould be antisymmetric under exchanges.
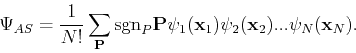
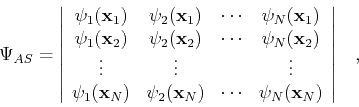
![]() and
and ![]() we have to sum over the spin variables:
we have to sum over the spin variables: