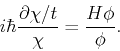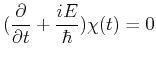Schödinger's Equation

According to the fourth postulate of quantum mechanics, the time evolution of the state function 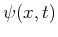$\psi(x,t)$ is determined by the so-called time dependent Schrödinger's equation:

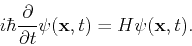$$i\hbar \frac{\partial}{\partial t} \psi({\bf x},t) = H\psi({\bf x},t).$$ (1)

The operator 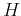$H$ is the Hamiltonian of the system. If 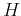$H$ is time-independent, we can separate this equatioon into spatial and time-dependent components:

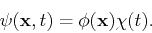$$\psi({\bf x},t) = \phi({\bf x})\chi(t).$$ (2)

By substituting into (1), we obtain:

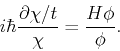$$i\hbar\frac{\partial \chi/t}{\chi}=\frac{H\phi}{\phi}.$$ (3)

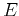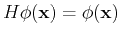This equation is satisfied if both sides are equal to a constant, that we call $E$:

$$H\phi({\bf x}) = \phi({\bf x})$$ (4)

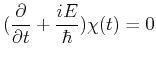$$(\frac{\partial}{\partial t} + \frac{iE}{\hbar}) \chi(t) = 0$$ (5)

The first of these equations is the time-independent or stationary Schödinger's equation. As we can see, 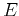$E$ is an eigenvalue of 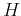$H$, and therefore we conclude that 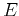$E$ is the energy of the system.

The second equation is simply solved to give us the oscillating form

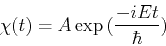$$\chi(t)=A\exp{(\frac{-iEt}{\hbar})}$$ (6)

Suppose that we solve the time-independent Schödinger's equation and obtain the eigenvalues and eigenfunctions

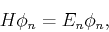$$H\phi_n=E_n\phi_n,$$ (7)

For each such solution there is a corresponding solution to the time-dependent Schödinger's equation

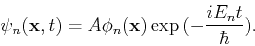$$\psi_n({\bf x},t) = A\phi_n({\bf x})\exp{(-\frac{iE_nt}{\hbar})}.$$ (8)

In cases with a discrete set of solutions, such as in a finite system, the subindex 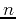$n$ is an integer. In cases where one obtains a continuum of solutions, we typically use the letter 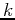$k$. For instance, in the case of a free particle in one dimension we have:

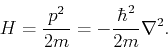$$H=\frac{p^2}{2m}=-\frac{\hbar^2}{2m}\nabla^2.$$ (9)

The time-independent Schrödinger's solution becomes

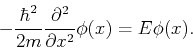$$-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}\phi(x)=E\phi(x).$$ (10)

The corresponding free-particle solutions are given by

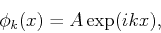$$\phi_k(x)=A\exp(ikx),$$ (11)

with eigenvalue (energy)

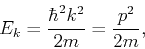$$E_k=\frac{\hbar^2k^2}{2m}=\frac{p^2}{2m},$$ (12)

where the momentum of the particle is 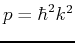$p=\hbar^2k^2$.

The solution to the time-dependent Schrödinger's equation will be given by

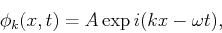$$\phi_k(x,t)=A\exp{i(kx-\omega t)},$$ (13)

where we have labeled

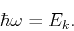$$\hbar\omega = E_k.$$ (14)