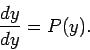In th eprevious section we learned how to generate random deviates with a
uniform probability distribution in an interval ![]() . This
distributioon is normalized, so that
. This
distributioon is normalized, so that
Now, suppose that we generate a sequence ![]() and we take some
function of it to generate
and we take some
function of it to generate
![]() . This new sequence is
going to be distributed according to some probaility density
. This new sequence is
going to be distributed according to some probaility density ![]() , such
that
, such
that
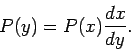
If we want to generate a desired normalized distribution ![]() , we need
to solve the differential equation:
, we need
to solve the differential equation: