


Next: Exercise 8.1: Single-slit diffraction
Up: Time dependent Schrödinger equation
Previous: Time dependent Schrödinger equation
The Schrödinger equation (81) can be integrated in a formal
sense to obtain:
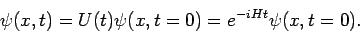 |
(82) |
From here we deduce that the wave function can be evolved forward in time
by applying the time-evolution operator
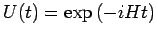 :
:
Likewise, the inverse of the time-evolution operator moves the wave
function back in time:
where we have use the property
Although it would be nice to have an algorithm based on the direct
application of 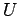 , it has been shown that this is not stable. Hence, we
apply the following relation:
, it has been shown that this is not stable. Hence, we
apply the following relation:
Now, the derivatives with recpect to 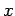 can be approximated by
can be approximated by
The time evolution operator is approximated by:
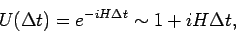 |
(85) |
with an error of the order of 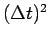 .
Replacing the expression (82) for
.
Replacing the expression (82) for 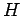 , we obtain:
, we obtain:
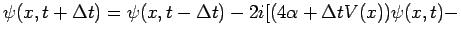 |
|
|
(86) |
![$\displaystyle \alpha(\psi(x+\Delta x,t)+\psi(x-\Delta x,t))],$](img674.png) |
|
|
(87) |
with
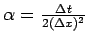 .
.
The probability of finding an electron at 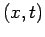 is given by
is given by
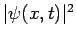 . This equations do no conserve this probability exactly,
but the error is of the order of
. This equations do no conserve this probability exactly,
but the error is of the order of 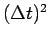 . The convergence can be
determined by using smaller steps.
. The convergence can be
determined by using smaller steps.
Subsections



Next: Exercise 8.1: Single-slit diffraction
Up: Time dependent Schrödinger equation
Previous: Time dependent Schrödinger equation
Adrian E. Feiguin
2004-06-01
![]() is given by
is given by
![]() . This equations do no conserve this probability exactly,
but the error is of the order of
. This equations do no conserve this probability exactly,
but the error is of the order of ![]() . The convergence can be
determined by using smaller steps.
. The convergence can be
determined by using smaller steps.