


Next: Exercise 7.1: Verification
Up: Electrostatic potentials
Previous: Units
Suppouse that we are given the values of 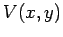 in the boundaries of a
rectangular area. If we divide the rectangle in a grid, we can the apply
(78) to calculate the values of
in the boundaries of a
rectangular area. If we divide the rectangle in a grid, we can the apply
(78) to calculate the values of 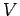 inside. However, we
notice right away that if we apply this equation in a point in the middle,
we get zero as a result. So the first obvious observation is that the
initial estimate for the method can not be a constant value.
It is evident now that the procedure has
to be iterative. We start from the bottom-left corner, and we sweep across
the grid. As we obtain the first estimate for
inside. However, we
notice right away that if we apply this equation in a point in the middle,
we get zero as a result. So the first obvious observation is that the
initial estimate for the method can not be a constant value.
It is evident now that the procedure has
to be iterative. We start from the bottom-left corner, and we sweep across
the grid. As we obtain the first estimate for 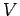 , we repeat the sweep
until the values of
, we repeat the sweep
until the values of 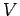 do not change considerably, and we can say that we
have converged with certain accuracy. Here we have started with the
initial
values
do not change considerably, and we can say that we
have converged with certain accuracy. Here we have started with the
initial
values 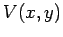 inside the grid that in principle can be any initial
guess (exept a constant, as we have seen). The rate of convergence will
be determined by the proximity of this guess to the actual solution.
inside the grid that in principle can be any initial
guess (exept a constant, as we have seen). The rate of convergence will
be determined by the proximity of this guess to the actual solution.
The algorithm can be decribed as follows:
- Divide the rgion of interest into a grid. The region must be
enclosed by boundaries with known values of
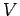 .
.
- Assingn to all points of the boundary the given values, and all
interior cells an arbitrary potential (preferably a reasonable guess)
- sweep the internal cells by rows or columns and calculate the
new values of
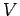 as the average in the four neighboring points.
as the average in the four neighboring points.
- Repeat the sweep using the values obtained in the previous
iteration, until the potential does not change within certain level of
accuracy.
Subsections



Next: Exercise 7.1: Verification
Up: Electrostatic potentials
Previous: Units
Adrian E. Feiguin
2004-06-01