MD simulation: Continuous potentials

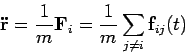
The interaction between hard particles was considered as an instantaneous collision process, with forces of infinite strength actin instantaneously during infinitely short times. A dynamical equation is of no use in such model, and it was therefore appropriate to calculate the collision laws to obtain the new velocities. In between collisions, the particles fly freely without acceleration. In contrast, for a continuous varying potential, the particles are either in a force field, or interact with some other particle at long distances and at any time. Therefore

$$\mathbf{\ddot{r}}=\frac{1}{m}\mathbf{F}_{i}=\frac{1}{m}\sum_{j\neq i}\mathbf{% f}_{ij}(t)$$

with

$$\mathbf{f}_{ij}=-\nabla _{i}V(r_{ij})$$

where $V$ is the interaction potential (e.g. Lennard-Jones).

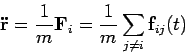
When evaluating the total force acting on a particle we apply periodic boundary conditions and the nearest image convention. In this way we may determine the sum of all the forces acting on a particle. A popular method to integrate the equations of motion is the Verlet algorithm:

$$\mathbf{r}_{i}(t_{n+1})=2\mathbf{r}_{i}(t_{n})-\mathbf{r}_{i}(t_{n-1})+% \mathbf{F}_{i}(t_{n})(\Delta t)^{2}$$

(Notice that this is not a self starting algorithm)