Next: Monte Carlo simulation of
Up: The Ising model
Previous: Boundary conditions
The net magnetic moment or ``magnetization' 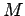 is given by
is given by
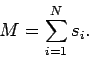 |
(115) |
Usually we are interested in the average
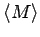 and the
fluctuations
and the
fluctuations
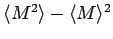 as a function of
the temperature of the system and the applied magnetic field. We can
determine the temperature as a function of the energy of the system in two
ways. One way is to measure the probability that the demon has an energy
as a function of
the temperature of the system and the applied magnetic field. We can
determine the temperature as a function of the energy of the system in two
ways. One way is to measure the probability that the demon has an energy
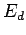 . An easier way to determine the temperature is to measure the mean
demon energy. However, since the values of the demon energy are not
continuous for the Ising model, the temperature is not proportional to the
mean demon energy as it is for the ideal gas. It can be shown that in the
limit of an infinite system, the temperature for
. An easier way to determine the temperature is to measure the mean
demon energy. However, since the values of the demon energy are not
continuous for the Ising model, the temperature is not proportional to the
mean demon energy as it is for the ideal gas. It can be shown that in the
limit of an infinite system, the temperature for 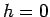 is related to
is related to 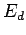 by
by
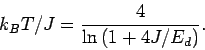 |
(116) |
This results is obtained by replacing the integrals by sums over all the
possible demon energies. Note that in the limit 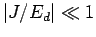 , this
reduces to
, this
reduces to 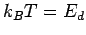 as expected.
as expected.



Next: Monte Carlo simulation of
Up: The Ising model
Previous: Boundary conditions
Adrian E. Feiguin
2004-06-01